؟Naive Bayes Classifier كيف يعمل

Naive Bayes Classifier هو أحد أنواع الـprobabilistic classifiers ومبني على تطبيق بسيط ومباشر لأحد أهم نظريات الاحتمالات: Bayes theorem. ورغم إنه يضع افتراض بسيط وفي الغالب غير مناسب للـdata لكنه سريع ومرن وبيقدم نتائج جيدة ويستخدم في الكثير من التطبيقات كـbaseline.

لكن إزاي ممكن نستخدم Bayes theorem في الـclassification؟

لنفترض إن X عبارة data point، وإن X ممكن تنتمي لواحد من 2 classes وهم$y_{1}, y_{2}$ ، ممكن خلال Bayes theorem أقدر أحسب احتمال أن X تنتمي لـ $y_{1}$ واحتمال انها تنتمي لـ $y_{2}$ كالآتي: $$ P(y_{1}|X) = \frac{P(X|y_{1})×P(y_{1})}{P(X)}, \hspace{5mm} P(y_{2}|X) = \frac{P(X|y_{2})×P(y_{2})}{P(X)} $$ الفكرة الرئيسية في Bayes theorem هي إنك من الـdata بتبني اعتقاد مبدأي (Prior Belief) عن كل class، بعد كده لما تشوف data points (Evidence) هتغير من اعتقادك المبدأي للاعتقاد جديد (Posterior Belief) وذلك بناء على مدى صحة الـevedence (Likelihood).

إزاي بيحصل الكلام ده؟

في البداية أول معلومة تقدر تتعلمها من الـdata هي احتمال ظهور كل class في الداتا $P(y_{1}),P(y_{2})$، وهو ده الـprior belief: إحتمال إن أي data point تنتمي للـclass الأول أو الثاني، والفكرة منه هي إن يبقى عندك اعتقاد مبدأي عن احتمال انتماء data point معينة لأي class قبل ما تعرف أي تفاصيل عن الـdata point دى.

خلينا نطرحها بمثال: لنفترض إننا بنحاول نفرق بين الـspam emails والـvalid emails، لما بصيت على الـdata لقيت إن 80% منها عبارة عن valid emails و 20% عبارة عن spam email. دلوقتي لو سألتك عن احتمال إن رسالة معينة تكون spam، بدون معرفة أي تفاصيل عن الرسالة، مش هتقدر تحكم عليها غير بالاعتقاد المبدأي الى كونته من الـdata المتاحة، وهو ده الـprior belief (P(spam)).

لكن لو بدأت اديلك بعض المعلومات (features) عن الرسالة، زى بعض الكلمات الموجودة في الرسالة أو مصدرها، هتبدأ تغير اعتقادك المبدأي، لإنك لقيت evidence يرجح كفة class عن الأخرى، لتصل إلى اعتقاد جديد (Posterior belief P(spam|features)).

لكن بأي نسبة هيتغير اعتقادك الجديد عن اعتقادك المبدأي؟ هيتغير بنسبة مدى صحة الـevidence على اعتبار إن الرسالة دى فعلا spam. وده ما يسمى بالـlikelihood (P(features|spam)).

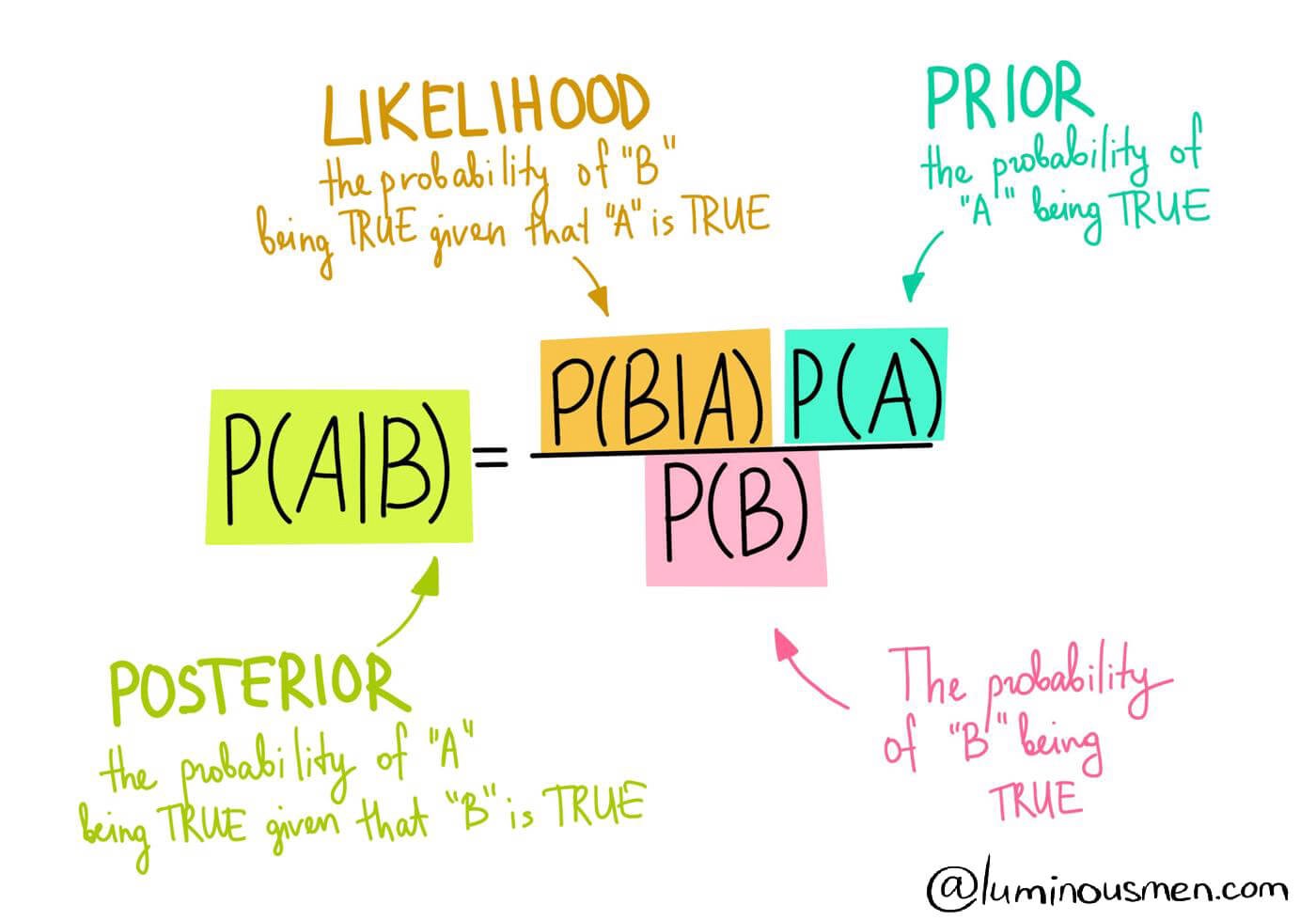
Fig 1: Bayes Rule.
Source: Click here

بناء على المثال ده، نقدر نمثل Bayes Rule بالمعادلة التالية: $$ Posterior = \frac{Likelihood×Prior}{Evidence} $$

حتى الآن كل الى عملناه هو تطبيق Bayes Rule بشكل مباشر، الخطوة التالية هى إننا نحسب كل term في المعادلة عشان نقدر نحسب الـposterior ونوصل لنتيجة.

الـPrior هو أسهل حاجة نقدر نحسبها في المعادلة، لإنه عبارة عن نسبة الـclass في الـdata، بالإضافة إلى إن لو عندك domain knowledge عن المشكلة قبل ما تبدأ تحلها، ممكن تستخدمها في إنك تحدد الـprior بنفسك.

بالنسبة للـ likelihood ($P(X|y_{k})$) فهنا لازم ناخد في الاعتبار إن X عبارة عن data point فيها أكتر من feature, بمعنى إن $X= (x_{1}, x_{2}, ...,x_{n})$ وبالتالي هنحسب $P(x_{1}, x_{2}, ...,x_{n}|y_{k})$. عشان نحسب الـterm هنستغل إننا نقدر نعبّر عن البسط كالآتي: $$ P(x_{1}, x_{2}, ...,x_{n}|y_{k})P(y_{k}) = P(y_{k},x_{1}, x_{2}, ...,x_{n}) $$ حيث أن $P(y_{k},x_{1}, x_{2}, ...,x_{n})$ تعبر عن الـjoint probability distribution بين الـclass وكل feature في الـdatapoint، من خلال الـdistribution ده ممكن نرتب الـvariables ونفكه من جديد باستخدام سلسلة من الـconditional probabilities: $$ P(x_{1}, x_{2}, ...,x_{n},y_{k}) = P(x_{1}| x_{2}, ...,x_{n},y_{k}) P(x_{2}, ...,x_{n},y_{k}) \hspace{70mm} \\ \rule{0mm}{5mm} \hspace{6mm} = P(x_{1}| x_{2}, ...,x_{n},y_{k}) P(x_{2}| x_{3}, ...,x_{n},y_{k}) P(x_{3}, ...,x_{n},y_{k})\\ \rule{0mm}{5mm} = ... \hspace{70mm} \\ \rule{0mm}{5mm} \hspace{28mm}= P(x_{1}| x_{2}, ...,x_{n},y_{k}) P(x_{2}| x_{3}, ...,x_{n},y_{k})... P(x_{n-1}|x_{n},y_{k}) P(x_{n}|y_{k})P(y_{k}) $$

دلوقتي عندنا أكتر من conditional probability term بين كل الـfeatures وبعضها بالإضافة للـclass كمان، هنحسبهم كلهم إزاي؟

Naive Bayes بيضع افتراض بسيط جداً عشان يحل المشكلة دى: بيفترض إن الـfeatures مستقلة عن بعضها، بمعني إن مفيش أي علاقة تربط كل feature بالآخرى. الإفتراض الساذج ده هو سبب تسميته بـNaive classifier، لإنه لا يضع اعتبار للعلاقة بين كل feature والأخرى. لكنه بيبسّط المعادلة السابقة للشكل ده: $$ P(x_{1}, x_{2}, ...,x_{n},y_{k}) = P(x_{1}|\cancel{ x_{2}, ...,x_{n}},y_{k}) P(x_{2}| \cancel{x_{3}, ...,x_{n}},y_{k})... P(x_{n-1}|\cancel{x_{n}},y_{k}) P(x_{n}|y_{k})P(y_{k}) \\ \rule{0mm}{5mm} = P(x_{1}|y_{k})P(x_{2}|y_{k})...P(x_{n}|y_{k})P(y_{k}) \hspace{22mm} \\ \rule{0mm}{7mm} = P(y_{k})\prod_{i=1}^{n} P(x_{i}|y_{k}) \hspace{46mm} $$ بالنسبة للـevidence (P(X))، فممكن نستغل ميزة إن الـclasses كلها disjoint (الـsample لا يمكن أن تنتمي لأكتر من class واحد في نفس الوقت)ونحسبه عن طريق الـmarginal probability كالآتي:

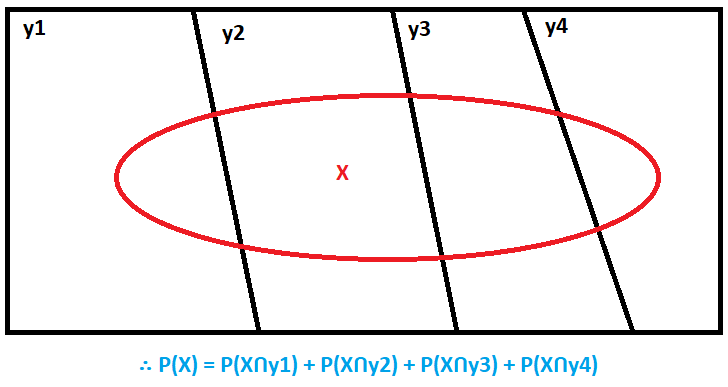
Fig 2: Marginal Probability Rule.

$$ P(X) = \sum_{j=1}^{k} P(X,y_{j}) = \sum_{j=1}^{k} P(X|y_{j})P(y_{j}) $$ وبناءً على افتراض الـindependence، نقدر نبسّط المعادلة السابقة بنفس الطريقة: $$ P(X) = \sum_{j=1}^{k} P(X|y_{j})P(y_{j}) = \sum_{j=1}^{k}P(x_{1}, x_{2}, ...,x_{n},y_{k}) = \sum_{j=1}^{k} (P(y_{j})\prod_{i=1}^{n} P(x_{i}|y_{j})) $$ ليصبح الشكل النهائي لمعادلة Bayes كالتالي: $$ P(y_{k}|X) = \frac{P(y_{k}) \prod_{i=1}^{n} P(x_{i}|y_{k})}{\sum_{j=1}^{k} (P(y_{j}) \prod_{i=1}^{n} P(x_{i}|y_{j}))} $$ الى نقدر نلاحظه من المعادلة دى هو إن المقام ثابت بغض النظر عن الـclass الى بنحسب الـprobability الخاصة بها، فبالتالي لو انا مش مهتم بالـprobability الخاصة بكل class وكل هدفي إن انا اعرف اي class تنتمي له X، فمش ضروري أحسب المقام وهكتفي بحساب البسط فقط: $$ P(y_{k}|X) \propto{P(y_{k}) \prod_{i=1}^{n} P(x_{i}|y_{k})} \\ \therefore \text{Predicted Class } (\hat{y}) = argmax_{y_k} (P(y_{k}) \prod_{i=1}^{n} P(x_{i}|y_{k})) $$ الملاحظة الثانية هى إن حتى الآن كل الشغل ده لا يضع أي افتراض عن علاقة الـfeatures بالـclass، بمعني آخر إحنا حتى الآن محددناش ايه هو الـprobability distribution الخاص بـ $P(x_{i}|y_{k})$ ، وهنا تظهر مرونة Naive Bayes كـclassifier: لإن الـdistribution ده إحنا الى بنحدده على حسب الـfeatures، فعلى سبيل المثال لو عندي categorical features فممكن اعتبر إن $P(x_{i}|y_{k})$ هى نسبة ظهور $x_{i}$ في $y_{k}$.

أما لو كان عندي Numerical features فممكن افترض إن $P(x_{i}|y_{k})$ عبارة عن Gaussian distribution واحسبه كالتالي: $$ P(x_{i}|y_{k}) = \frac{1}{\sqrt{2\pi\sigma_{k}}}e^{\frac{-1}{2} (\frac{x-\mu_{k}}{\sigma_{k}})^2} $$ حيث أن $\mu_{k}, \sigma_{k}$ هي الـmean و الـstandard deviation الخاص بقيم $x_{i}$ التي تنتمي إلى $y_{k}$ .

وحتى لو كان الـgaussian distribution غير ملائم للداتا فممكن تستخدم أي طريقة من طرق الـkernel density estimation عشان توصل لـdistribution أفضل وتستخدمه.

ولو افترضت إن الـdistribution هو multinomial distribution هنتجه إلى الـmulitinumial naive bayes وهو أحد أشهر الـmodels المستخدمة في الـtext classification.

مزايا وعيوب Naive Bayes:

Naive Bayes هو بالأصل probabilistic classifier وبالتالي بيستفيد جداً من الـdomain knowledge الى ممكن تقدمها له كـpriors أو كـdistribution للـlikelihood وممكن يحقق نتائج جيدة جداً بكمية data صغيرة, بالإضافة إلى أن الـtraining سريع لإنه بيتم عن طريق closed form formula، وبالتالي مفيش iterations و parameters updates.

لكن على الجانب الآخر، ف افتراض الـindependence وهو نادر الحدوث في أي real dataset بيؤثر على أداءه، بالرغم من إنه ممكن يطلع نتائج جيدة حتى لو كان فيه dependence بين الـfeatures، وبالتالي نقدر نقول إن naive bayes يعاني من high bias/low variance.

مشكلة آخرى ممكن تحدث تسمى بالـZero-frequency problem، وبتحصل لو كانت أحد الـfeatures لا تظهر في أحد الclasses على الإطلاق، وبالتالي تصبح الـlikelihood الخاصة بها صفر، ده بيؤدي إلى إن أي sample تحتوي الـfeature دى مش هيكون عندها أي احتمال إنها تنتمي للـclass دى بغض النظر عن باقي قيم الـfeatures.

المشكلة دى ممكن نحلها عن طريق الـlaplacian smoothing وهو إننا نضيف 1 على الـcount الخاص بكل feature في كل الـclasses بحيث تكون كل الـfeatures موجودة في كل الـclasses, وعشان نحافظ على الـprobability distribution, هنضيف على المقام عدد الـones الى ضفناهم على كل الـfeatures عشان يكون مجموع الـprobabilities بواحد.

لمزيد من المعلومات: