؟Activation functionsالخيار الشائع للـ ReLUليه أصبحت الـ
؟Activationsوايه يميزها عن باقي الـ
ReLU هو اختصار Rectified Linear Unit وهي واحدة من أكثر الـactivation functions المستخدمة في الـNeural networks، رغم إن اسمها يحتوى على كلمة linear لكنها non linear function، وده واضح رياضياً وحتى من الرسم بتاعها، لكن ليه بتقدر تنافس الـactivation functions الأخرى المكوّنة من smooth curves رغم إنها حرفياً عبارة عن خطين بس؟
$$ ReLU=max(0,x) $$
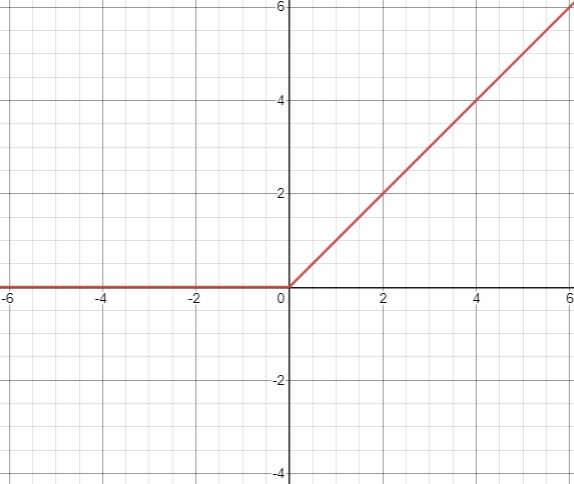
Fig 1: ReLU Graph
ميزة الـReLU الكبرى مش بتظهر لما أستخدم واحدة بس منها، لكن بتكون واضحة لما أجمع شوية دوال ReLU كتير مع بعض، نقطة الانكسار الموجودة بين جزئين دالة الـReLU بتقدر تقرّبلك مجموعة الخطوط الكتيرة دى من أي منحنى أنت عايزه عن طريق إنها بتتيح لك تكسر الخط المستقيم في أي مكان انت عايزه (أو المكان الى الـneural network بتتعلمه).
لاحظ الصورة التالية: لما استخدمت ReLU واحدة بس مقدمتش اختلاف كبير عن الـstraight line، لكن لما بدأت اعمل nesting واجمعهم مع بعض بدأت أكوّن شكل جديد مقدرتش أوصله لما جمعت الـstraight lines مع بعض.
وبالنسبة للـNeural networks، في الصورة التالية نقدر نلاحظ إن neural network بتستخدم ReLU كـActivation function وصلت لمنحنى قريب من المنحنى التانج عن neural network بتستخد $tanh$ في نفس عدد الـepoch
لاحظ الصورة التالية: لما استخدمت ReLU واحدة بس مقدمتش اختلاف كبير عن الـstraight line، لكن لما بدأت اعمل nesting واجمعهم مع بعض بدأت أكوّن شكل جديد مقدرتش أوصله لما جمعت الـstraight lines مع بعض.
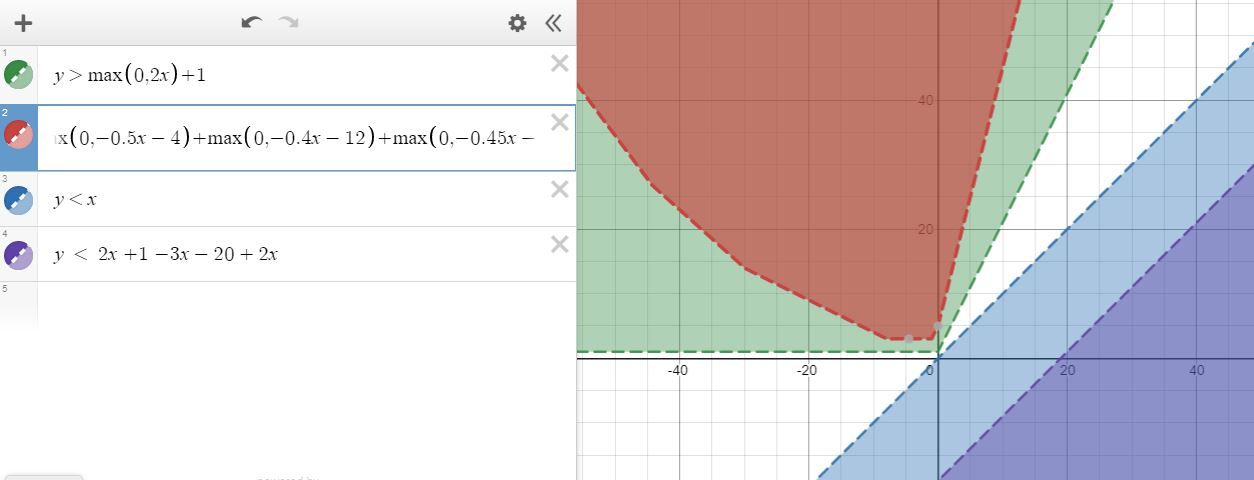
Fig 2: ReLU vs. Linear function
طيب هل هي فعلاً تقدر توصل لمنحنيات صعبة زى باقي الـactivation function؟
الإجابة القصيرة: نعم، وده واضح من خلال استخدامها الشائع والواسع في كل مجالات الـdeep learning، لاحظ الصورة التالية: عن طريق استخدام أكتر من ReLU function قدرت أوصل لشكل تقريبي من منحنى $x^3+x^2-x-1$
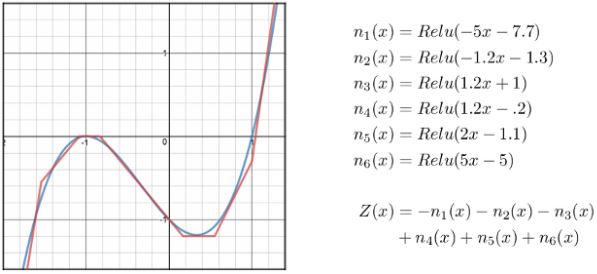
Fig 3: We can use many ReLUs to approximate complex functions
Source: Click here
وبالنسبة للـNeural networks، في الصورة التالية نقدر نلاحظ إن neural network بتستخدم ReLU كـActivation function وصلت لمنحنى قريب من المنحنى التانج عن neural network بتستخد $tanh$ في نفس عدد الـepoch
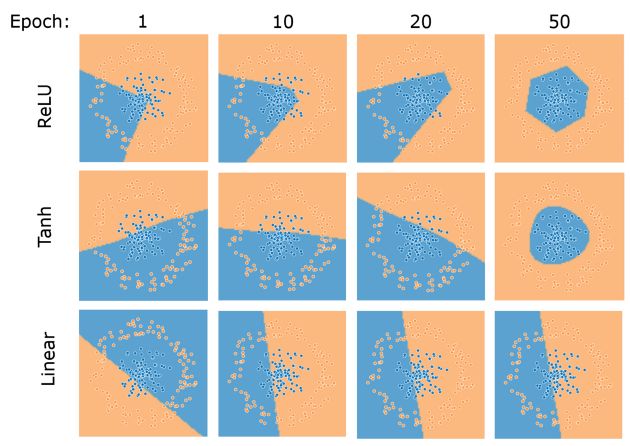
Fig 4: كل network تحتوي 3 hidden layers، كل منهم يحتوى 3 neurons
Source: Click here
طيب ما الـtanh وصلت لـsmooth curve وعملت نتيجة كويسة بردو، ليه اروح للـReLU؟
هنا تيجي ميزة الـReLU التانية والى بتديلها أفضلية كبيرة عن الـtanh: إنها very computationally efficient، هي في الآخر عبارة عن خط وتفاضلها ثابت، على عكس الـtanh الى فيها exponentials وتفاضلها متغير.
لمزيد من المعلومات