؟ConvNetsفي الـ Backpropagationكيف يتم تنفيذ الـ
Fully Connected Neural Networksوكيف يختلف في تنفيذه عن الـ
في الغالب كانت بداية معرفتك بالـbackbropagation عن طريق شرحه على Fully connected neural network, لكن بعد ما تتطرق لأشكال أخرى من الـneural netowrks مثل الـconvolutional neural network بتلاقي إن الـbackpropagation مستخدم فيهم كـalgorithm رئيسي لحساب الـgradients في كل layer لكن بدون ذكر تفاصيل أكثر عنها، لإنك بالفعل غير مضطر لمعرفة تفاصيل الرياضية قبل استخدامها، ومع ذلك فمعرفة كيف تتم داخل الـConv layers قد يكون سؤال مر ببالك ولو من باب الفضول في وقت من الأوقات.
Note
جميع الصور والـAnimation مصدرها هو المقال الرائع ده والى بيتكلم عن الـbackpropagation في الـconvnets بشكل مبسط وجيد جداً، أنصح بقراءته لمزيد من التفاصيل.
Tip
يفضّل أن يكون لديك معرفة كافية بخطوات الـbackpropagation واستخدام الـderivatives والـchain rule فيه قبل قراءة المقال.
إذاً كيف يتم تنفيذ الـBackpropagation في الـConvNets؟
لنفترض إن عندنا Input $X_{3×3}$ و Filter $F_{2×2}$ كالتالي: $$X_{3×3} = \left( \begin{array}{ccc} X_{11}&X_{12}&X_{13} \\ X_{21}&X_{22}&X_{23} \\ X_{31}&X_{32}&X_{33} \\ \end{array} \right) \hspace{10mm} F_{2×2} = \left( \begin{array}{cc} F_{11}&F_{12} \\ F_{21}&F_{22} \\ \end{array} \right) $$ في الـforward pass نحصل على ناتج الـconvolution بين $X$ و $F$ (على اعتبار ان الـstride=1 ,والـpadding=0) وهو $O_{2×2}$ ،و تتم العملية كالتالي: $$\underbrace{\left( \begin{array}{cc} O_{11}&O_{12} \\ O_{21}&O_{22} \\ \end{array} \right)}_{O_{2×2}} = \underbrace{\left( \begin{array}{ccc} X_{11}&X_{12}&X_{13} \\ X_{21}&X_{22}&X_{23} \\ X_{31}&X_{32}&X_{33} \\ \end{array} \right)}_{X_{3×3}} \otimes \underbrace{\left( \begin{array}{cc} F_{11}&F_{12} \\ F_{21}&F_{22} \\ \end{array} \right)}_{F_{2×2}} $$
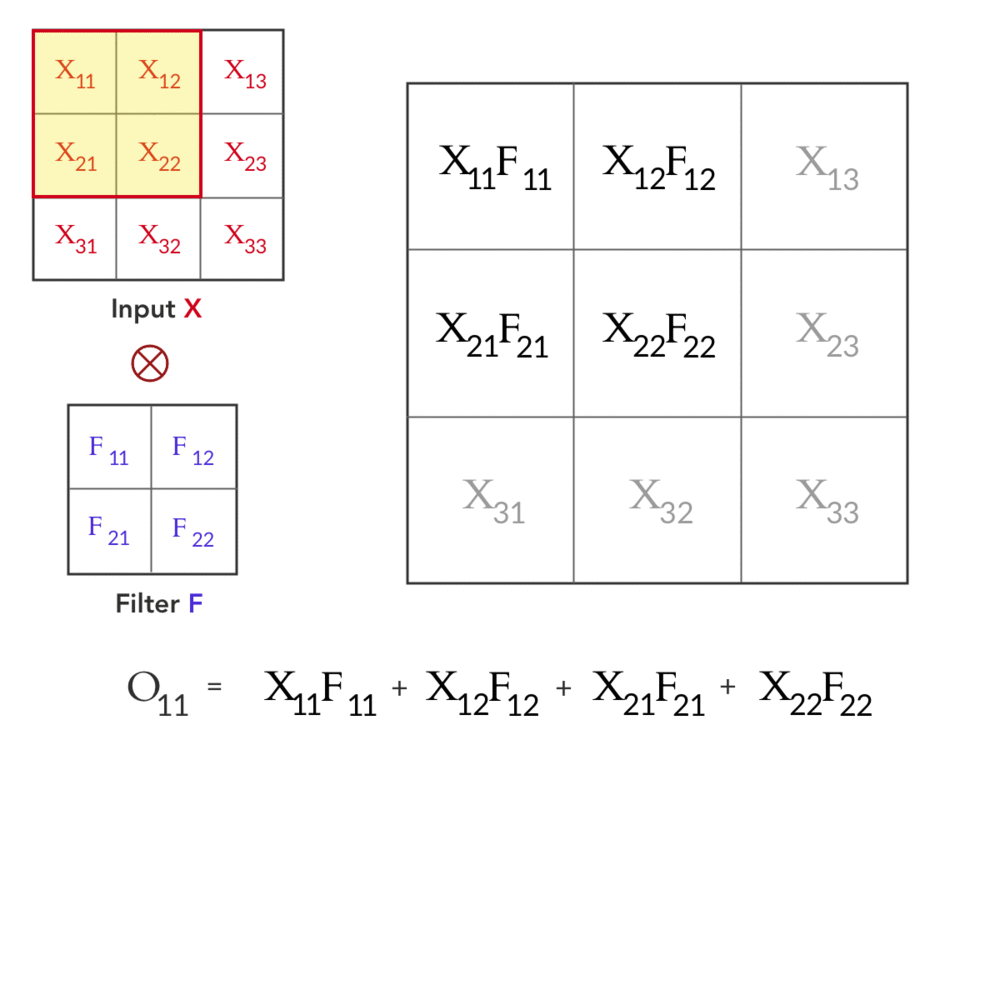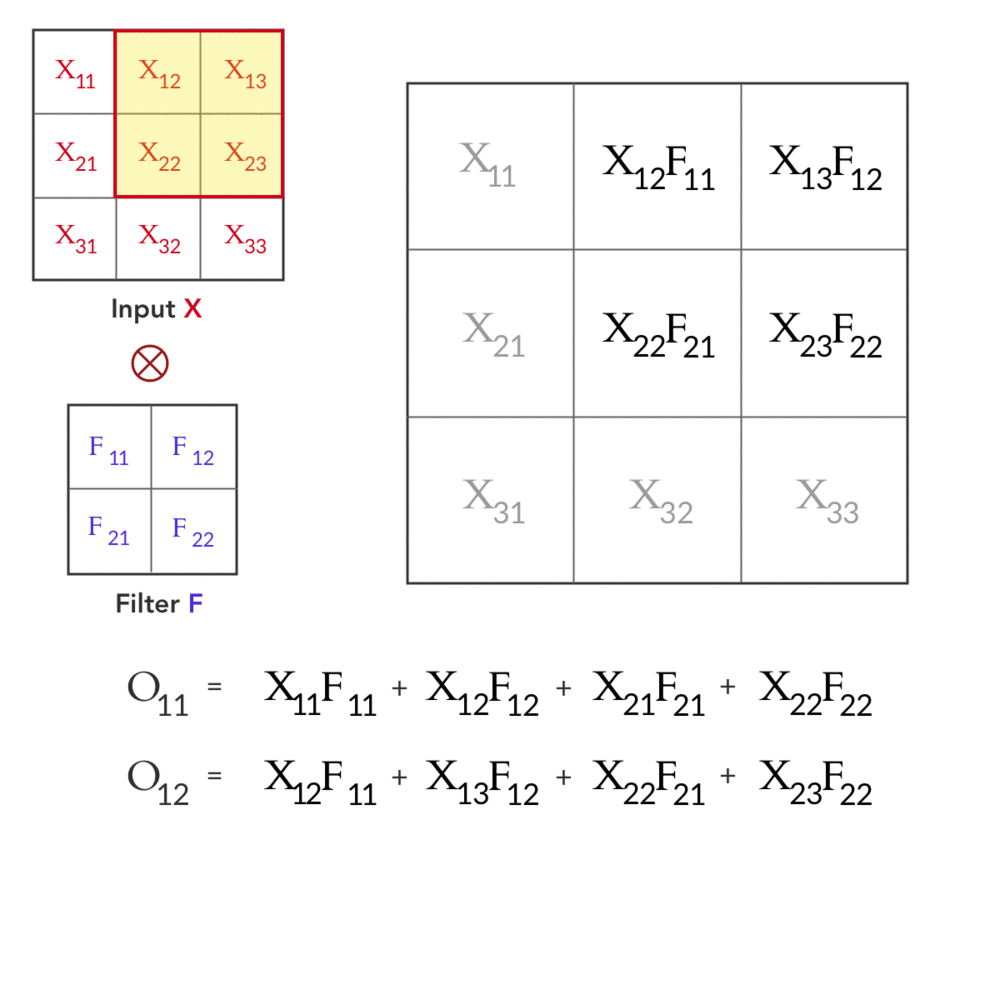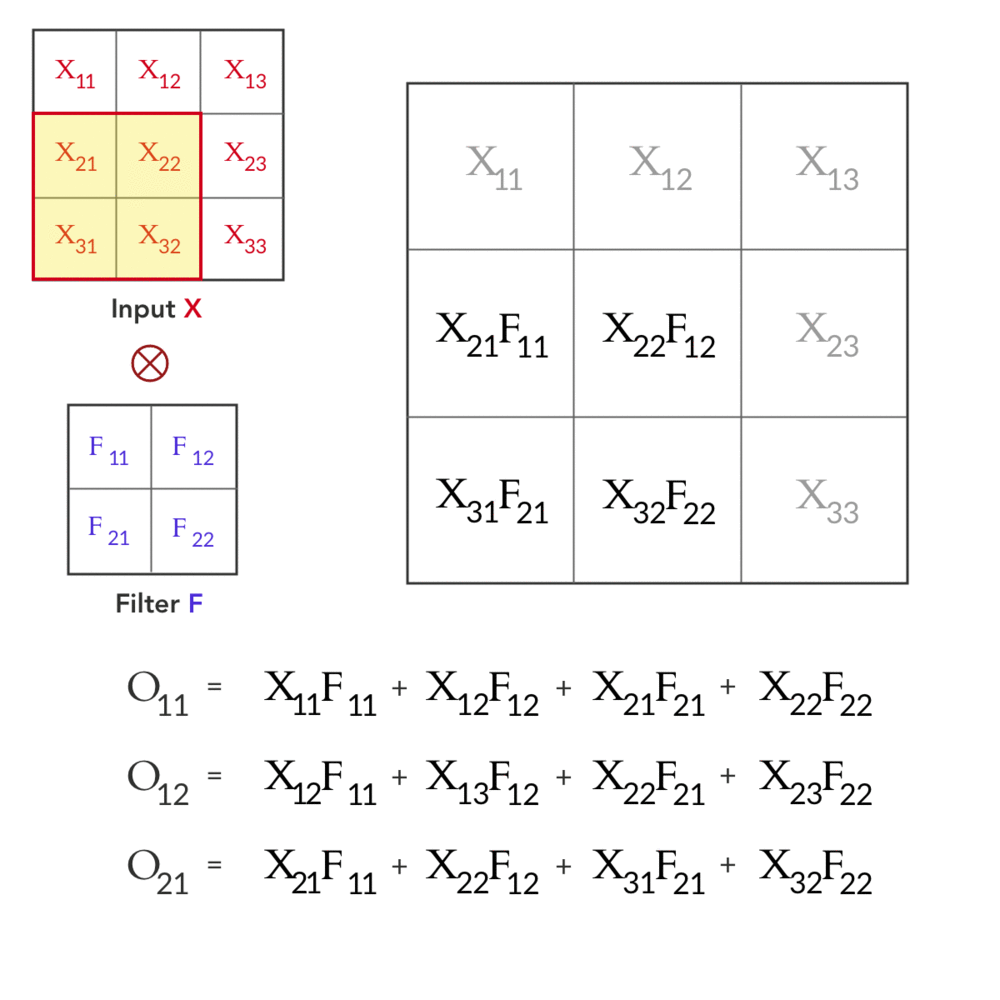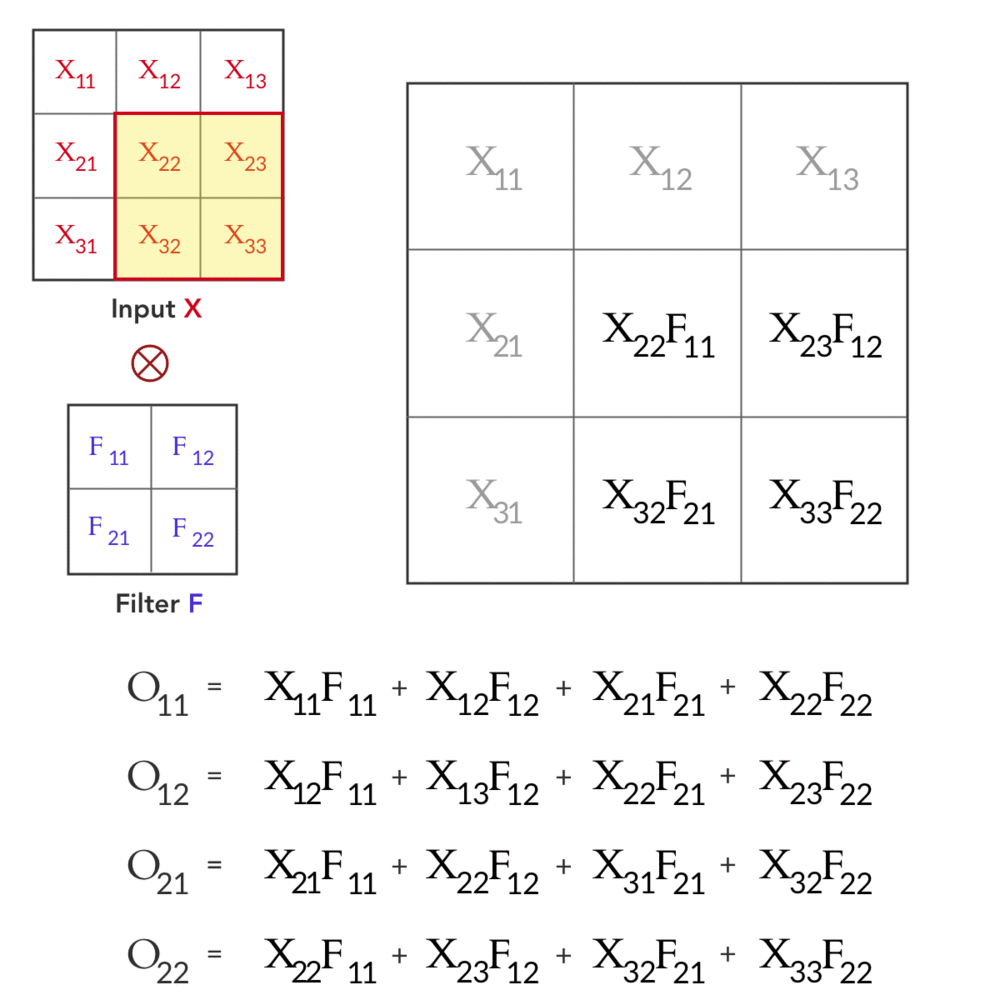
Fig 1: Forward pass in a convolution layer with one filter
عملية الـBackpropagation (موضّحة في Fig 2) تتم عن طريق الـChain rule، بنبدأ من آخر layer ونحسب الـloss gradient $\frac{\partial L}{\partial z}$ بتاعها ونتحرك للـlayer الى قبلها. في الlayer التالية بنحسب الـloss gradient عندها عن طريق ضرب $\frac{\partial L}{\partial z}$ في الـlocal gradients الخاصة بالـlayer وهي كل من $\frac{\partial z}{\partial x}$ و $\frac{\partial z}{\partial y}$.
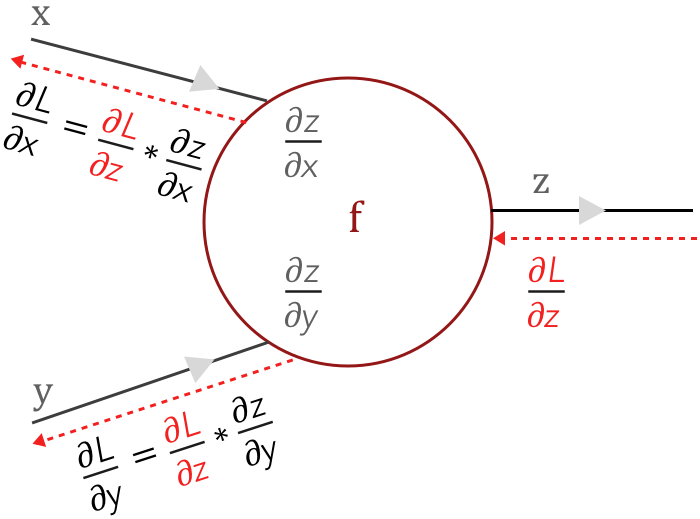
Fig 2: Gradients flow in a neuron
في الـfully connected neural network، حساب الـlocal gradients يتم بطريقة مباشرة لأن z عبارة عن دالة في كل من x,y، لكن في الـconvolutional neural network نجد أن O عبارة عن ناتج convolution بين الـweights (الـfilter parameters) والfeature map X.
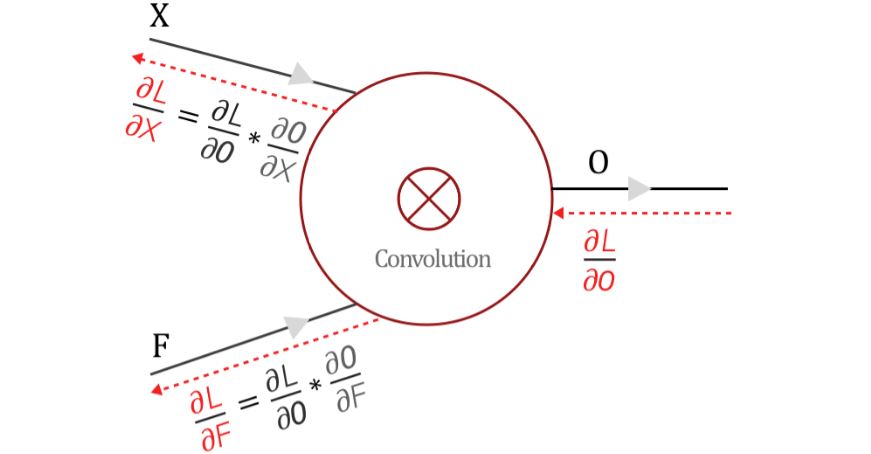
Fig 3: Gradients flow in a convolutional neuron
ليه بنحتاج نحسب الـlocal gradients في الـconvolution؟
$\frac{\partial O}{\partial F}$ بنستخدمه عشان نحسب الـloss gradient بالنسبة لـF، وهو ده الى بنستخدمه عشان نعمل update لقيم الـfilter: $$ \frac{\partial L}{\partial F} = \frac{\partial O}{\partial F} × \frac{\partial L}{\partial O} \\ \rule{0mm}{7mm} F_{updated} = F - \alpha \frac{\partial L}{\partial F} $$ أما بالنسبة لـ $\frac{\partial O}{\partial X}$، بما أن X هى output الـlayer السابقة، إذاً يصبح$\frac{\partial L}{\partial X}$ هو الـloss gradient الخاص بالـlayer السابقة، وبالتالي بنحسبه عشان نكمل الـbackpropagation في باقي الـlayers. $$ \frac{\partial L}{\partial X} = \frac{\partial O}{\partial X} × \frac{\partial L}{\partial O} $$
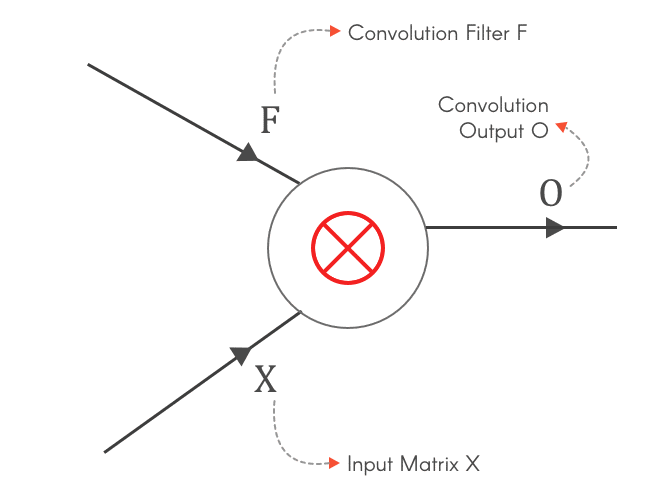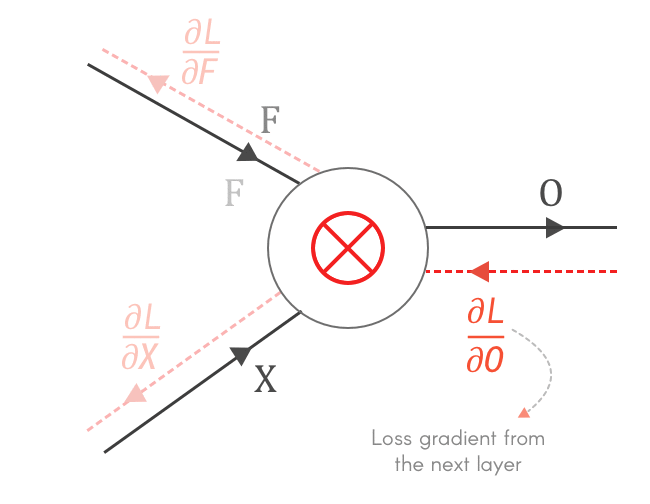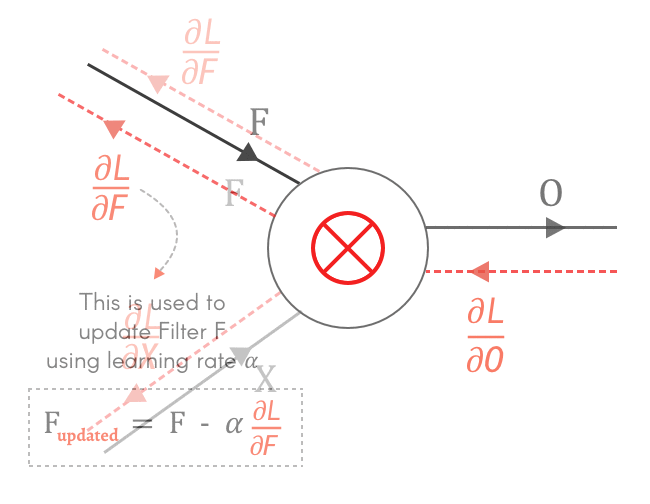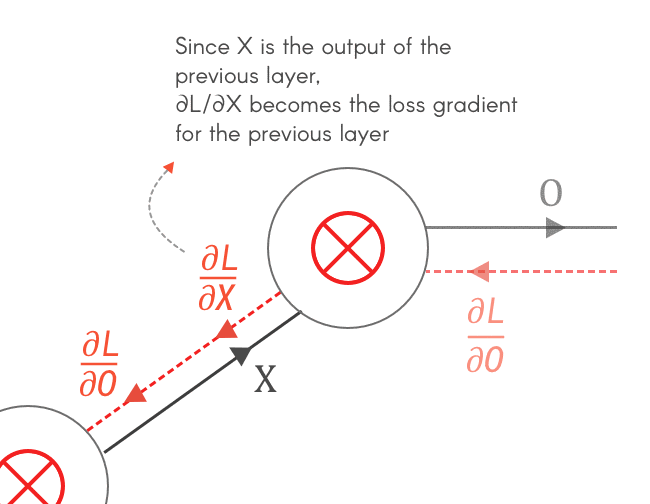
Fig 4: Why do we need to calculate $\frac{\partial L}{\partial X}, \frac{\partial L}{\partial F}$
إزاي هنحسب $\frac{\partial L}{\partial F}$؟
في البداية عشان نحسب $\frac{\partial L}{\partial F}$، هنحتاج نحسب الـlocal gradient الخاص بيها وهو $\frac{\partial O}{\partial F}$، العلاقة بين O و F الى هنحسب منها الـgradient هى: $$\underbrace{\left( \begin{array}{cc} O_{11}&O_{12} \\ O_{21}&O_{22} \\ \end{array} \right)}_{O_{2×2}} = \underbrace{\left( \begin{array}{ccc} X_{11}&X_{12}&X_{13} \\ X_{21}&X_{22}&X_{23} \\ X_{31}&X_{32}&X_{33} \\ \end{array} \right)}_{X_{3×3}} \otimes \underbrace{\left( \begin{array}{cc} F_{11}&F_{12} \\ F_{21}&F_{22} \\ \end{array} \right)}_{F_{2×2}} $$ عشان نحسب $\frac{\partial O}{\partial F}$ لازم نحسب الـgradient الخاص بـO بالنسبة لكل element في F، على سبيل المثال لو حسبنا الـgradient الخاص بـO بالنسبة إلى $F_{11}$: $$ O_{11} = X_{11}F_{11} + X_{12}F_{12} + X_{21}F_{21} + X_{22}F_{22} \\ \rule{0mm}{7mm} O_{12} = X_{12}F_{11} + X_{13}F_{12} + X_{22}F_{21} + X_{23}F_{22} \\ \rule{0mm}{7mm} O_{21} = X_{21}F_{11} + X_{22}F_{12} + X_{31}F_{21} + X_{32}F_{22} \\ \rule{0mm}{7mm} O_{22} = X_{22}F_{11} + X_{23}F_{12} + X_{32}F_{21} + X_{33}F_{22} \\ \rule{0mm}{10mm} \frac{\partial O_{11}}{\partial F_{11}} = X_{11}, \hspace{5mm} \frac{\partial O_{12}}{\partial F_{11}} = X_{12}, \hspace{5mm} \frac{\partial O_{21}}{\partial F_{11}} = X_{21}, \hspace{5mm} \frac{\partial O_{22}}{\partial F_{11}} = X_{22}\\ \rule{0mm}{10mm} \therefore \frac{\partial O}{\partial F_{11}} = \left( \begin{array}{cc} \frac{\partial O_{11}}{\partial F_{11}}&\frac{\partial O_{12}}{\partial F_{11}} \\\rule{0mm}{5mm} \frac{\partial O_{21}}{\partial F_{11}}&\frac{\partial O_{22}}{\partial F_{11}} \\ \end{array} \right) = \left( \begin{array}{cc} X_{11}&X_{12} \\ X_{21}&X_{22} \end{array} \right) $$ وبالمثل نقدر نحسب الـgradient بالنسبة لكل من $F_{21}, F_{12}, F_{22}$: $$ \frac{\partial O}{\partial F_{12}} = \left( \begin{array}{cc} X_{12}&X_{13} \\ X_{22}&X_{23} \end{array} \right), \hspace{5mm} \frac{\partial O}{\partial F_{21}} = \left( \begin{array}{cc} X_{21}&X_{22} \\ X_{31}&X_{32} \end{array} \right), \hspace{5mm} \frac{\partial O}{\partial F_{22}} = \left( \begin{array}{cc} X_{22}&X_{23} \\ X_{32}&X_{33} \end{array} \right) $$ دلوقتي نقدر نطبق قاعدة الـChain rule عشان نحسب $\frac{\partial L}{\partial F}$: $$ \frac{\partial L}{\partial F} = \frac{\partial O}{\partial F} × \frac{\partial L}{\partial O} $$
إزاي هنطبق الـchain rule على مصفوفات؟
عشان نحسب المعادلة دى، هنحسب الـ loss gradient بالنسبة لكل element في F على حدة باستخدام المعادلة الآتية:
$$
\frac{\partial L}{\partial F_{ij}} = \left\langle \frac{\partial L}{\partial O}, \frac{\partial O}{\partial F_{ij}} \right\rangle_{F}
$$
حيث أن $\langle\cdot,\cdot\rangle_{F}$ تعبّر عن الـFrobenius inner product بين مصفوفتين.
ماهو Frobenius Inner Product؟
$$
\text{Let }
A = \left( \begin{array}{cc}
A_{11}&A_{12} \\
A_{21}&A_{22}
\end{array} \right), \hspace{5mm}
B = \left( \begin{array}{cc}
B_{11}&B_{12} \\
B_{21}&B_{22}
\end{array} \right) \\ \rule{0mm}{8mm}
\therefore \langle A,B\rangle_{F} = A_{11}B_{11} + A_{12}B_{12} + A_{21}B_{21} + A_{22}B_{22}
$$
$\frac{\partial L}{\partial O}$ ممكن نحسبه بسهولة عن طريق تفاضل الـloss function بالنسبة لكل عنصر في O لو كان O هو ناتج آخر layer في الـnetwork، أما لو كان ناتج layer في وسط الnetwork هيكون عبارة عن الـloss gradient القادم من الـlayer التالية لها.
$$
\frac{\partial L}{\partial O} = \left( \begin{array}{cc}
\frac{\partial L}{\partial O_{11}}&\frac{\partial L}{\partial O_{12}} \\ \rule{0mm}{5mm}
\frac{\partial L}{\partial O_{21}}&\frac{\partial L}{\partial O_{22}} \\
\end{array} \right)
$$
الآن نقدر نحسب الـloss gradient بالنسبة لكل عنصر في F:
$$
\frac{\partial L}{\partial F_{11}} = \frac{\partial L}{\partial O_{11}} \frac{\partial O_{11}}{\partial F_{11}} + \frac{\partial L}{\partial O_{12}} \frac{\partial O_{12}}{\partial F_{11}} + \frac{\partial L}{\partial O_{21}} \frac{\partial O_{21}}{\partial F_{11}} + \frac{\partial L}{\partial O_{22}} \frac{\partial O_{22}}{\partial F_{11}} \\
\rule{0mm}{10mm}
\frac{\partial L}{\partial F_{12}} = \frac{\partial L}{\partial O_{11}} \frac{\partial O_{11}}{\partial F_{12}} + \frac{\partial L}{\partial O_{12}} \frac{\partial O_{12}}{\partial F_{12}} + \frac{\partial L}{\partial O_{21}} \frac{\partial O_{21}}{\partial F_{12}} + \frac{\partial L}{\partial O_{22}} \frac{\partial O_{22}}{\partial F_{12}} \\
\rule{0mm}{10mm}
\frac{\partial L}{\partial F_{21}} = \frac{\partial L}{\partial O_{11}} \frac{\partial O_{11}}{\partial F_{21}} + \frac{\partial L}{\partial O_{12}} \frac{\partial O_{12}}{\partial F_{21}} + \frac{\partial L}{\partial O_{21}} \frac{\partial O_{21}}{\partial F_{21}} + \frac{\partial L}{\partial O_{22}} \frac{\partial O_{22}}{\partial F_{21}} \\
\rule{0mm}{10mm}
\frac{\partial L}{\partial F_{22}} = \frac{\partial L}{\partial O_{11}} \frac{\partial O_{11}}{\partial F_{22}} + \frac{\partial L}{\partial O_{12}} \frac{\partial O_{12}}{\partial F_{22}} + \frac{\partial L}{\partial O_{21}} \frac{\partial O_{21}}{\partial F_{22}} + \frac{\partial L}{\partial O_{22}} \frac{\partial O_{22}}{\partial F_{22}} \\
\rule{0mm}{5mm}
$$
لو عوّضنا عن كل $\frac{\partial O_{xy}}{\partial F_{ij}}$ بالقيم الى حسبناها فوق:
$$
\frac{\partial L}{\partial F_{11}} = \frac{\partial L}{\partial O_{11}} X_{11} + \frac{\partial L}{\partial O_{12}} X_{12} + \frac{\partial L}{\partial O_{21}} X_{21} + \frac{\partial L}{\partial O_{22}} X_{22} \\
\rule{0mm}{10mm}
\frac{\partial L}{\partial F_{12}} = \frac{\partial L}{\partial O_{11}} X_{12} + \frac{\partial L}{\partial O_{12}} X_{13} + \frac{\partial L}{\partial O_{21}} X_{22} + \frac{\partial L}{\partial O_{22}} X_{23} \\
\rule{0mm}{10mm}
\frac{\partial L}{\partial F_{21}} = \frac{\partial L}{\partial O_{11}} X_{21} + \frac{\partial L}{\partial O_{12}} X_{22} + \frac{\partial L}{\partial O_{21}} X_{31} + \frac{\partial L}{\partial O_{22}} X_{32} \\
\rule{0mm}{10mm}
\frac{\partial L}{\partial F_{22}} = \frac{\partial L}{\partial O_{11}} X_{22} + \frac{\partial L}{\partial O_{12}} X_{23} + \frac{\partial L}{\partial O_{21}} X_{32} + \frac{\partial L}{\partial O_{22}} X_{33} \\
\rule{0mm}{10mm}
$$
هل لاحظت إحنا بنعمل إيه؟ لاحظ إن ناتج الـchain rule الى طبقناها مشابه لناتج عملية الـconvolution الى كنا بنطبقها في الـforward pass! تعالى نكتب المعادلات الى وصلنا لها بصيغة convolution operation عشان نتأكد:
$$
\underbrace{\left( \begin{array}{cc}
\frac{\partial L}{\partial F_{11}}&\frac{\partial L}{\partial F_{12}} \\ \rule{0mm}{5mm}
\frac{\partial L}{\partial F_{21}}&\frac{\partial L}{\partial F_{22}} \\
\end{array} \right)}_{\frac{\partial L}{\partial F}} =
\underbrace{\left( \begin{array}{ccc}
X_{11}&X_{12}&X_{13} \\
X_{21}&X_{22}&X_{23} \\
X_{31}&X_{32}&X_{33} \\
\end{array} \right)}_{X_{3×3}} \otimes
\underbrace{\left( \begin{array}{cc}
\frac{\partial L}{\partial O_{11}}&\frac{\partial L}{\partial O_{12}} \\ \rule{0mm}{5mm}
\frac{\partial L}{\partial O_{21}}&\frac{\partial L}{\partial O_{22}} \\
\end{array} \right)}_{\frac{\partial L}{\partial O}}
$$
ناتج الـconvolution هو الأربع معادلات الى وصلنا لهم، وده يخلينا نستنتج إن الـconv layer بتطبق الـconvolution operation في الـforward pass عشان تحسب الـfeature maps، وفي الـbackward pass عشان تحسب الـgradients.
ماهو Frobenius Inner Product؟
$$
\text{Let }
A = \left( \begin{array}{cc}
A_{11}&A_{12} \\
A_{21}&A_{22}
\end{array} \right), \hspace{5mm}
B = \left( \begin{array}{cc}
B_{11}&B_{12} \\
B_{21}&B_{22}
\end{array} \right) \\ \rule{0mm}{8mm}
\therefore \langle A,B\rangle_{F} = A_{11}B_{11} + A_{12}B_{12} + A_{21}B_{21} + A_{22}B_{22}
$$
بعد ما حسبنا $\frac{\partial L}{\partial F}$ هنشوف دلوقتي إزاي نحسب $\frac{\partial L}{\partial X}$
$$\underbrace{\left( \begin{array}{cc} O_{11}&O_{12} \\ O_{21}&O_{22} \\ \end{array} \right)}_{O_{2×2}} = \underbrace{\left( \begin{array}{ccc} X_{11}&X_{12}&X_{13} \\ X_{21}&X_{22}&X_{23} \\ X_{31}&X_{32}&X_{33} \\ \end{array} \right)}_{X_{3×3}} \otimes \underbrace{\left( \begin{array}{cc} F_{11}&F_{12} \\ F_{21}&F_{22} \\ \end{array} \right)}_{F_{2×2}} $$ بنفس الطريقة الى حسبنا بيها الـlocal gradient بالنسبة لـF، هنحسب الـlocal gradient بالنسبة لـX: $$ O_{11} = X_{11}F_{11} + X_{12}F_{12} + X_{21}F_{21} + X_{22}F_{22} \\ \rule{0mm}{7mm} O_{12} = X_{12}F_{11} + X_{13}F_{12} + X_{22}F_{21} + X_{23}F_{22} \\ \rule{0mm}{7mm} O_{21} = X_{21}F_{11} + X_{22}F_{12} + X_{31}F_{21} + X_{32}F_{22} \\ \rule{0mm}{7mm} O_{22} = X_{22}F_{11} + X_{23}F_{12} + X_{32}F_{21} + X_{33}F_{22} \\ \rule{0mm}{10mm} \frac{\partial O_{11}}{\partial X_{11}} = F_{11}, \hspace{5mm} \frac{\partial O_{12}}{\partial X_{11}} = 0 \\ \rule{0mm}{8mm} \frac{\partial O_{21}}{\partial X_{11}} = 0, \hspace{8mm} \frac{\partial O_{22}}{\partial X_{11}} = 0 \\ \rule{0mm}{10mm} \therefore \frac{\partial O}{\partial X_{11}} = \left( \begin{array}{ccc} \frac{\partial O_{11}}{\partial X_{11}}&\frac{\partial O_{12}}{\partial X_{11}} \\\rule{0mm}{5mm} \frac{\partial O_{21}}{\partial X_{11}}&\frac{\partial O_{22}}{\partial X_{11}} \\ \end{array} \right) = \left( \begin{array}{cc} F_{11}&0 \\ 0&0 \end{array} \right) $$ وبالمثل نقدر نحسب الـgradient بالنسبة لكل من لباقي عناصر X: $$ \frac{\partial O}{\partial X_{12}} = \left( \begin{array}{cc} F_{12}&F_{11} \\ 0&0 \end{array} \right), \hspace{5mm} \frac{\partial O}{\partial X_{13}} = \left( \begin{array}{cc} 0&F_{12} \\ 0&0 \end{array} \right), \hspace{5mm} \frac{\partial O}{\partial X_{21}} = \left( \begin{array}{cc} F_{21}&0 \\ F_{11}&0 \end{array} \right) \text{ ... etc} $$ بعد ما حسبنا الـlocal gradient بالنسبة لـX نقدر دلوقتي نطبق الـchain rule: $$ \frac{\partial L}{\partial X_{ij}} = \langle \frac{\partial L}{\partial O}, \frac{\partial O}{\partial X_{ij}} \rangle_{F} $$ بعد ما نحسب الـproduct ونعوّض هنلاقي النتائج التالية: $$ \frac{\partial L}{\partial X_{11}} = \frac{\partial L}{\partial O_{11}} F_{11} \hspace{80mm} \\ \rule{0mm}{8mm} \frac{\partial L}{\partial X_{12}} = \frac{\partial L}{\partial O_{11}} F_{12} + \frac{\partial L}{\partial O_{12}} F_{11} \hspace{62mm} \\ \rule{0mm}{8mm} \frac{\partial L}{\partial X_{13}} = \frac{\partial L}{\partial O_{12}} F_{12} \hspace{80mm} \\ \rule{0mm}{8mm} \frac{\partial L}{\partial X_{21}} = \frac{\partial L}{\partial O_{11}} F_{21} + \frac{\partial L}{\partial O_{21}} F_{11} \hspace{62mm} \\ \rule{0mm}{8mm} \frac{\partial L}{\partial X_{22}} = \frac{\partial L}{\partial O_{11}} F_{22} + \frac{\partial L}{\partial O_{12}} F_{21} + \frac{\partial L}{\partial O_{21}} F_{12} + \frac{\partial L}{\partial O_{22}} F_{11} \hspace{27mm} \\ \rule{0mm}{8mm} \frac{\partial L}{\partial X_{23}} = \frac{\partial L}{\partial O_{12}} F_{22} + \frac{\partial L}{\partial O_{22}} F_{12} \hspace{62mm} \\ \rule{0mm}{8mm} \frac{\partial L}{\partial X_{31}} = \frac{\partial L}{\partial O_{21}} F_{21} \hspace{80mm} \\ \rule{0mm}{8mm} \frac{\partial L}{\partial X_{32}} = \frac{\partial L}{\partial O_{21}} F_{22} + \frac{\partial L}{\partial O_{22}} F_{21} \hspace{62mm} \\ \rule{0mm}{8mm} \frac{\partial L}{\partial X_{33}} = \frac{\partial L}{\partial O_{22}} F_{22} \hspace{80mm} $$
المعادلات شكلها مختلف عن الى شفناه بالنسبة لـF، بس هل ممكن نعبّر عنها بـconvolution؟
نعم، نقدر نعبّر عنها عن طريق 'Full' Covolution بين F و $\frac{\partial L}{\partial O}$
Convolution Vs. Cross Correlation
على الرغم من إن الـconvolutional neural networks تحتوي في اسمها على كلمة convolution، إلا إن المسمى الفعلي للعملية الرياضية الى بتحصل فيها هو Cross Correlation, وهى إننا بنحرك الـfilter كsliding window على الـinput ونضرب العناصر المقابلة في بعضها ونجمع النتيجة، أما في الـConvolution بندوّر الـfilter بـ180 درجة الأول قبل ما نحركه.
عشان نطبق الـconvolution بالشكل الى هيطلع لي المعادلات دى لازم ندوّر الفلتر 180 درجة: $$ \left( \begin{array}{cc} F_{11}&F_{12} \\ F_{21}&F_{22} \\ \end{array} \right) \xRightarrow{180^o \text{-Rotation}} \left( \begin{array}{cc} F_{22}&F_{21} \\ F_{12}&F_{11} \\ \end{array} \right) $$ دلوقتي نقدر نحسب $\frac{\partial L}{\partial X}$ باستخدام full convolution، وهو يكافئ covolution with full zero padding: $$ \underbrace{\left( \begin{array}{ccc} \frac{\partial L}{\partial X_{11}}&\frac{\partial L}{\partial X_{12}}&\frac{\partial L}{\partial X_{13}}\\ \rule{0mm}{5mm} \frac{\partial L}{\partial X_{21}}&\frac{\partial L}{\partial X_{22}}&\frac{\partial L}{\partial X_{23}}\\ \rule{0mm}{5mm} \frac{\partial L}{\partial X_{31}}&\frac{\partial L}{\partial X_{32}}&\frac{\partial L}{\partial X_{33}}\\ \end{array} \right)}_{\frac{\partial L}{\partial X}} = \underbrace{\left( \begin{array}{cccc} 0&0&0&0 \\ \rule{0mm}{5mm} 0&\frac{\partial L}{\partial O_{11}}&\frac{\partial L}{\partial O_{12}}&0 \\ \rule{0mm}{5mm} 0&\frac{\partial L}{\partial O_{21}}&\frac{\partial L}{\partial O_{22}}&0 \\ \rule{0mm}{5mm} 0&0&0&0 \end{array} \right)}_{padded \frac{\partial L}{\partial O}} \otimes \underbrace{\left( \begin{array}{cc} F_{22}&F_{21} \\ F_{12}&F_{11} \\ \end{array} \right)}_{Rotated \hspace{1mm} F} $$
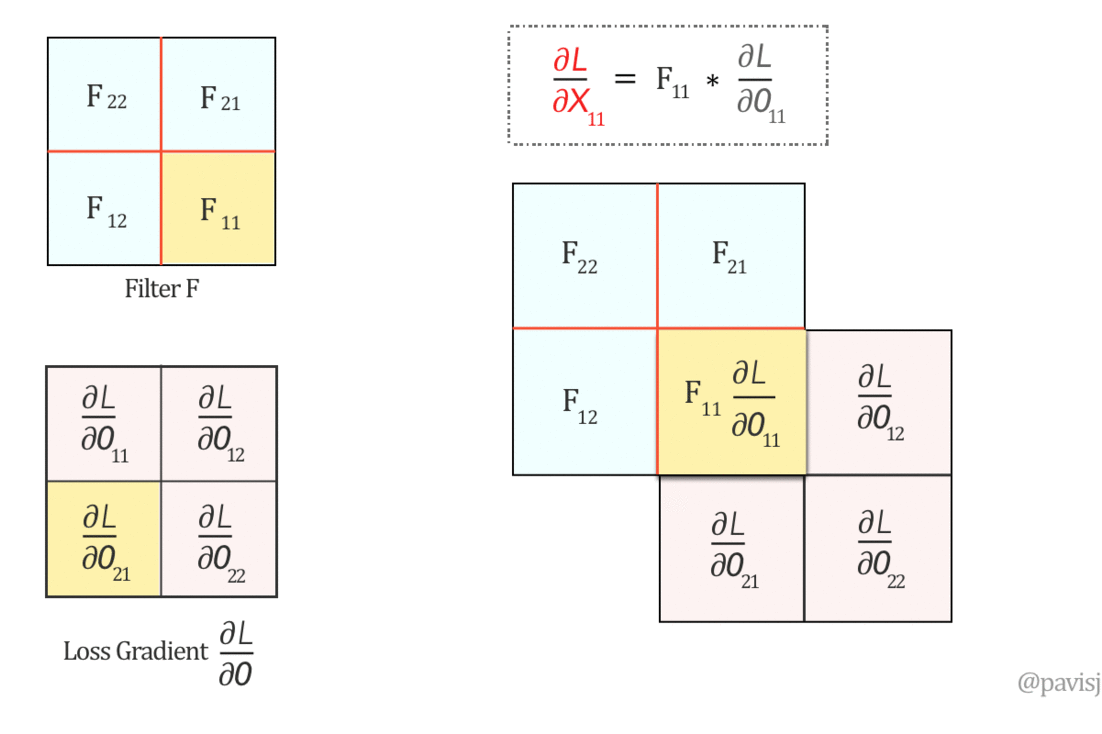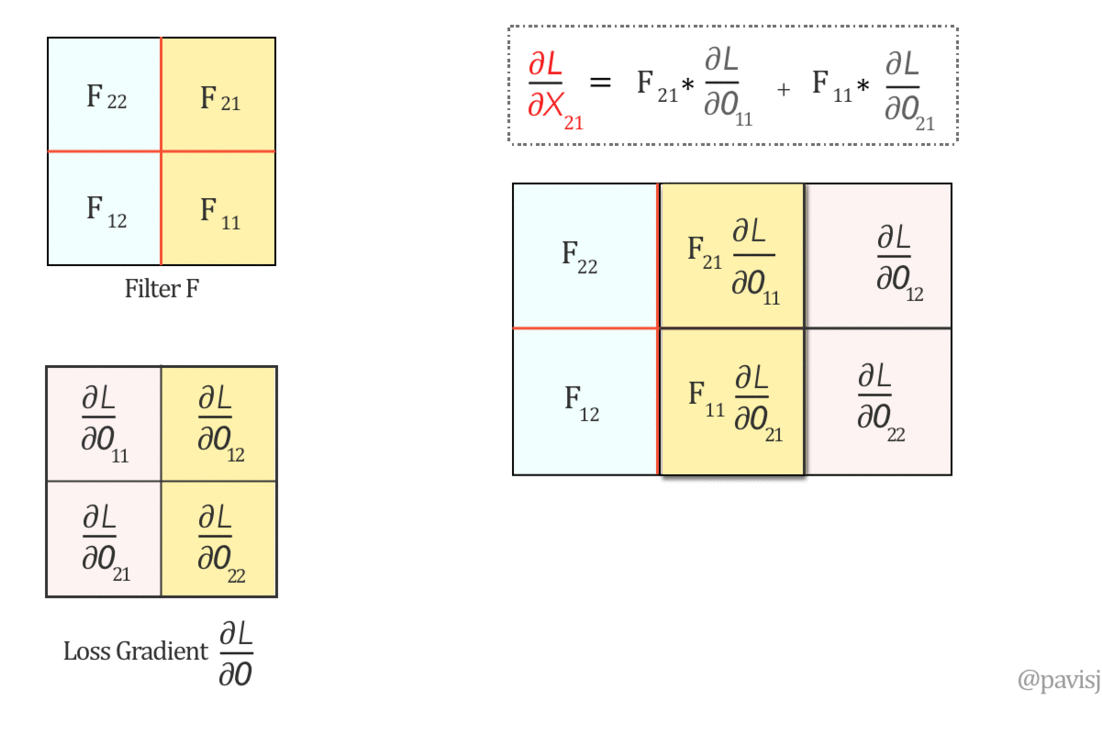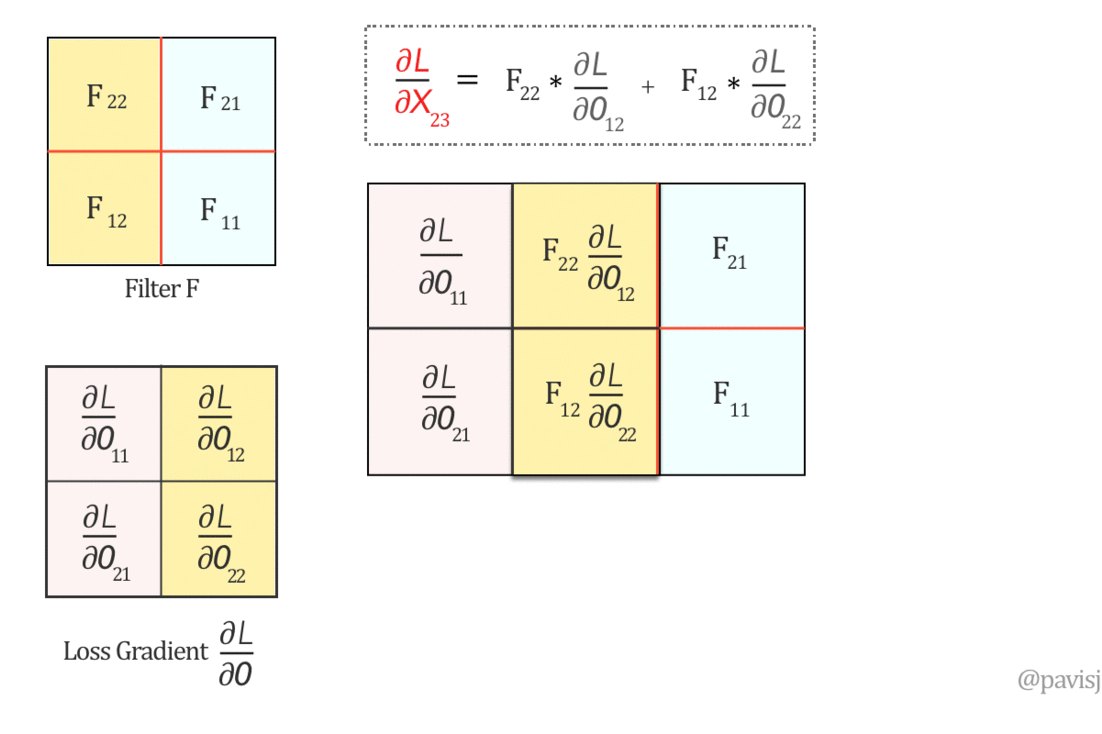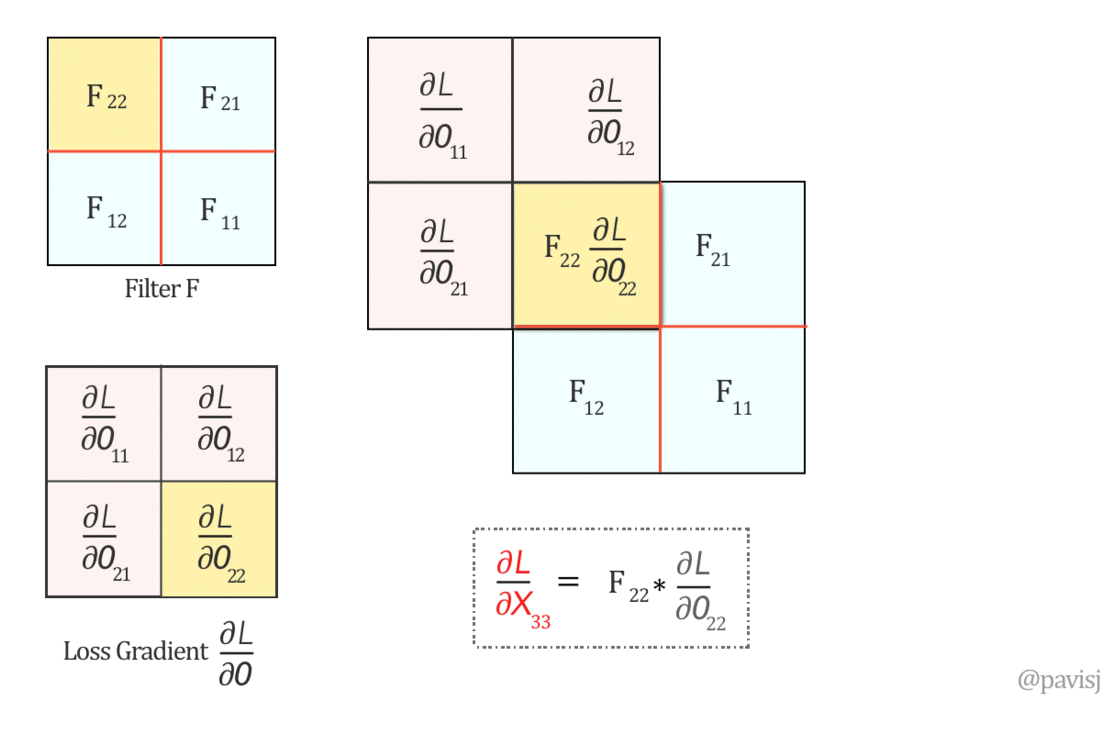
Fig 5: Full Convolution operation visualized between 180-degree flipped Filter F and loss gradient $\frac{\partial L}{\partial O}$
هل الـpooling layers بتأثر على الـbackpropagation؟
الـPooling layers لا تحتوي على learnable parametersو لكن زى ما لها دور في الـforward pass فبالتأكيد لها دور في الـbackward pass اثناء حساب الـgradients.
لنفترض إن الـinput الخاص بـ(2×2)pooling layer هو المصفوفة A, والـOutput هو المصفوفة B:
$$
A = \left( \begin{array}{cccc}
A_{11}&A_{12}&A_{13}&A_{14} \\
A_{21}&A_{22}&A_{23}&A_{24} \\
A_{31}&A_{32}&A_{33}&A_{34} \\
A_{41}&A_{42}&A_{43}&A_{44} \\
\end{array} \right), \hspace{5mm}
B = \left( \begin{array}{cc}
B_{11}&B_{12} \\
B_{21}&B_{22}\\
\end{array} \right) \\ \rule{0mm}{7mm}
B_{11} = pool\left( \begin{array}{cc}
A_{11}&A_{12} \\
A_{21}&A_{22}\\
\end{array} \right), \hspace{2mm}
B_{12} = pool\left( \begin{array}{cc}
A_{13}&A_{14} \\
A_{23}&A_{24}\\
\end{array} \right) \hspace{2mm}
\\ \rule{0mm}{7mm}
B_{21} = pool\left( \begin{array}{cc}
A_{31}&A_{32} \\
A_{41}&A_{42}\\
\end{array} \right), \hspace{2mm}
B_{22} = pool\left( \begin{array}{cc}
A_{33}&A_{34} \\
A_{43}&A_{44}\\
\end{array} \right) \hspace{2mm}
$$
أثناء الـbackpropagation هيبقى عندي $\frac{\partial L}{\partial B}$ ومنه هحتاج أحسب $\frac{\partial L}{\partial A}$ عشان يروح للـlayer الى وراه:
$$
\frac{\partial L}{\partial B} =
\left( \begin{array}{cc}
\frac{\partial L}{\partial B_{11}}&\frac{\partial L}{\partial B_{12}} \\ \rule{0mm}{5mm}
\frac{\partial L}{\partial B_{21}}&\frac{\partial L}{\partial B_{22}}
\end{array} \right)
$$
في حالة الـ Max pooling, عنصر واحد فقط من الأربعة هو الى بيعدي للـlayer التالية، وبالتالي هو العنصر الوحيد الى بيكون عنده قيمة للـgradient لإنه هو الوحيد الى شارك في الـerror.
لو أفترضنا إن $A_{11},A_{13},A_{31},A_{33}$ هم أكبر قيم في كل cell:
$$
\therefore \frac{\partial L}{\partial A} = \left( \begin{array}{cccc}
\frac{\partial L}{\partial B_{11}}&0&\frac{\partial L}{\partial B_{12}}&0 \\ \rule{0mm}{5mm}
0&0&0&0 \\ \rule{0mm}{5mm}
\frac{\partial L}{\partial B_{21}}&0&\frac{\partial L}{\partial B_{22}}&0 \\ \rule{0mm}{5mm}
0&0&0&0\\
\end{array} \right)
$$
أما في حالة الـAverage pooling، فكل عنصر بيشارك في الـerror بنفس القيمة، فبالتالي الـgradient بيتوزع عليهم بالتساوي:
$$
\therefore \frac{\partial L}{\partial A} = \frac{1}{4} \left( \begin{array}{cccc}
\frac{\partial L}{\partial B_{11}}&\frac{\partial L}{\partial B_{11}}&\frac{\partial L}{\partial B_{12}}&\frac{\partial L}{\partial B_{12}} \\ \rule{0mm}{5mm}
\frac{\partial L}{\partial B_{11}}&\frac{\partial L}{\partial B_{11}}&\frac{\partial L}{\partial B_{12}}&\frac{\partial L}{\partial B_{12}} \\ \rule{0mm}{5mm}
\frac{\partial L}{\partial B_{21}}&\frac{\partial L}{\partial B_{21}}&\frac{\partial L}{\partial B_{22}}&\frac{\partial L}{\partial B_{22}} \\ \rule{0mm}{5mm}
\frac{\partial L}{\partial B_{21}}&\frac{\partial L}{\partial B_{21}}&\frac{\partial L}{\partial B_{22}}&\frac{\partial L}{\partial B_{22}}\\
\end{array} \right)
$$
إذاً في النهاية ممكن نلخص الـbackpropagation في الـCNNs في خطوتين(بالإضافة إلى تأثير الـpooling على الـgradient flow):
$$ \frac{\partial L}{\partial F} = Convolution(\text{Input } X, \text{ Loss gradient } \frac{\partial L}{\partial O}) \hspace{25mm} \\ \rule{0mm}{8mm} \frac{\partial L}{\partial X} = \text{Full Convolution}(180^o \text{ Rotated filter } F, \text{ Loss gradient } \frac{\partial L}{\partial O}) $$
لمزيد من المعلومات: