؟Vanishing gradientsكيف نتعامل مع مشكلة الـ
ما أسبابها وما حلولها؟
الـVanishing Gradients هي أحد اكبر المشاكل الى أثرت على تطوّر الـneural networks لفترة طويلة، وبسببها كان تدريب الـdeep neural networks عملية صعبة وبتستغرق وقت كبير، لكن إيه السبب وراء المشكلة دى؟
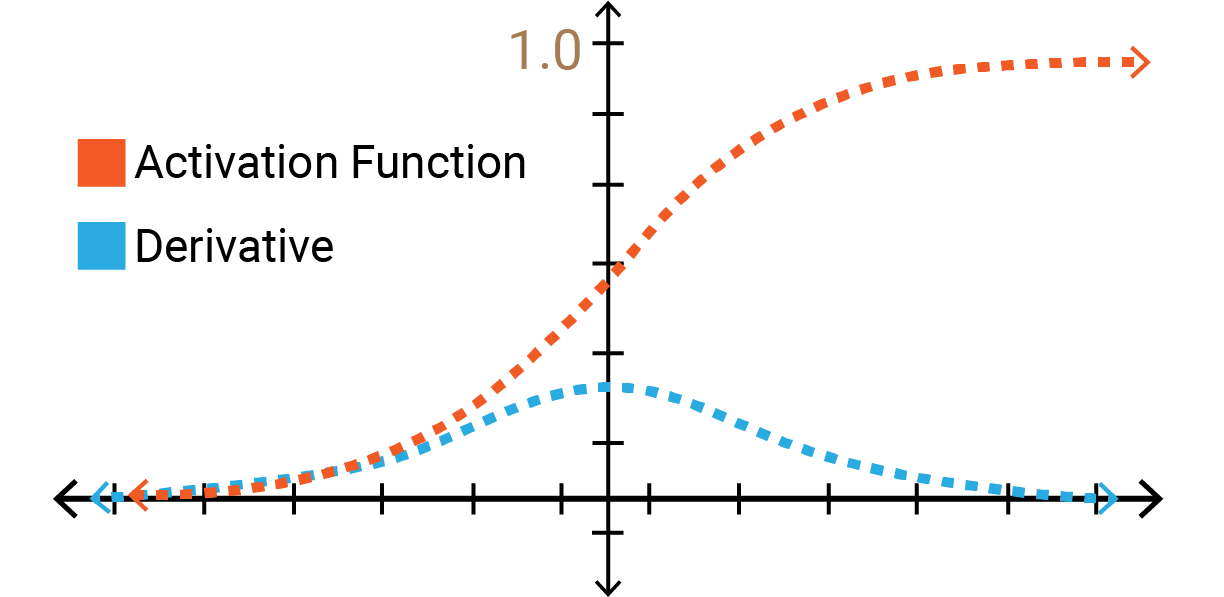
Fig 1: Vanishing gradients.
Source: Click here
أحد أسباب المشكلة هو الـrandom weights initialization عن طريق normal distribution الـmean بتاعه صفر والـvariance واحد، استخدام الطريقة دى مع activation function زى sigmoid أو tanh كان يؤدي إلى إن الـoutput variance في كل layer يكون أكبر من الـinput variance، ده كان بيسبّب إن الـsigmoid في الـlayers الآخيرة توصل للـsaturation (لاحظ Figure 2)، فيصبح الـgradient صغير جداً أو بصفر، بالتالي في الـbackpropagation مش هقدر أعمل updates والـlearning هياخد وقت كبير وممكن يتوقف تماماً.
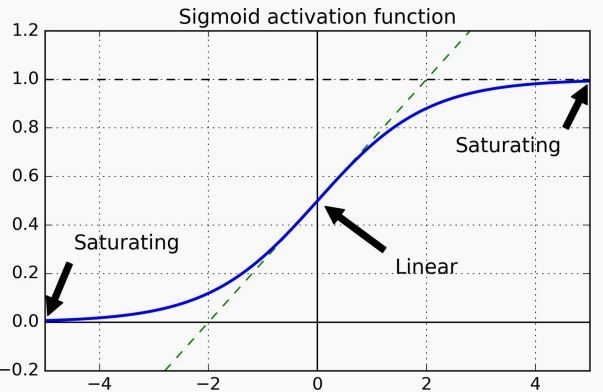
Fig 2: Sigmoid function saturation regions.
في Paper لـXavier Glorot، قال إن عشان نساوي الـinput variance والـoutput variance لازم يكون عدد الـinputs والـoutputs متساوي، لكنه قدم حل آخر يعوّض الشرط ده وهو الـGlorot initialization.
($fan_{out}$, $fan_{in}$ هو عدد الـinput neurons والـoutput neurons على الترتيب):
$\text{Where } fan_{avg} = (fan_{in} + fan_{out}/2), \text{ initialize weights with:}$
-
$\text{Normal Distribution with mean 0 and variance } \sigma^2 = \frac{1}{fan_{avg}}$
-
$\text{Or a uniform distribution between -r and +r with } r = \sqrt{\frac{3}{fan_{avg}}}$
طيب المشكلة دى ظهرت بسبب الـsaturation في sigmoid و tanh، هل ممكن احلها لو استخدمت ReLU؟
الـReLU بتحل المشكلة دى في الجزء الموجب، لكنها بتقدم مشكلة جديدة بسبب الجزء السالب; لإن لو كان الـinput بتاعها سالب هيكون الـoutput صفر، وكمان الـgradient صفر، فـ مش هيحصل update للـweights، وبالتالي في الـstep الجاية هيظل الـouput والـgradient صفر، هنا يقال إن الـneurons are dead: لإن مش هيحصل updates عندهم على الإطلاق.
الحل المباشر للمشكلة هو إننا نضيف قيمة للـfunction في الجزء السالب، فممكن نلجأ للـLeaky ReLU (موضحة في Figure 3); وفيها بنضيف ميل صغير جداً للـReLU في الجزء السالب، الميل ده إما يكون hyper parameter أنا الى بحدده، أو يكون رقم عشوائي في كل step (تُسمّى Randomized Leaky ReLU) وده بيضيف نوع من الـregularization على الـnetwork، أو يكون parameter بتتعلمه الـnetwork (تُسمّى Parametric Leaky ReLU) وده بيدي الـNetwork حرية أكبر، لكن ممكن يسبب overfitting لو الـdataset مش كبيرة بشكل كافي.
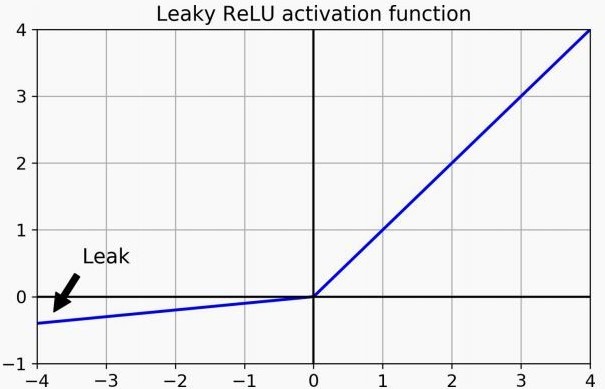
Fig 3: Leaky ReLU activation function.
وممكن نلجأ للـELU (موضّحة في Figure 4): وفيها الجزء السالب من الـReLU بياخد شكل الـexponential function، ورغم إنها ابطأ من الـReLU في الحساب، لكنها بتوصل للـconvergence في عدد خطوات أقل، لذلك في الـtraining بشكل عام بتكون اسرع، لكن في الـtesting فالـReLU بالتأكيد أسرع.
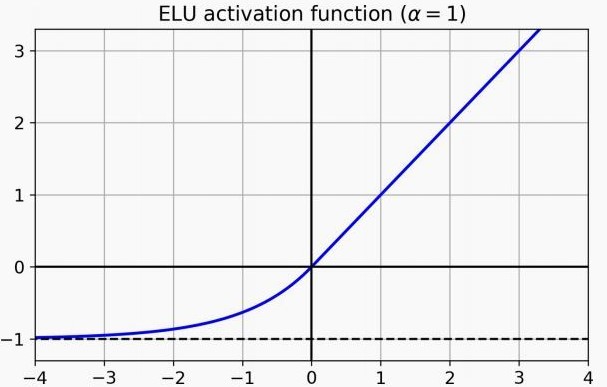
Fig 4: ELU activation function.
حتى الآن تعرضنا لبعض حلول الـVanishing gradients عن طريق الـGlorot initialization والـNon saturating activations زى الـReLU ومشتقاتها، لكن الحلول دى بتقيّد تصميم الـnetwork بالشروط الى بحطها على اختيار الـactivation وكمان بتعتمد بشكل كبير على الـinitialization.
هل ممكن نتفادى القيود دى؟
أحد الأسباب الى ممكن تؤدى إلى unstable training هو الـInternal Covariate shift: ومعناه إن الـinput distribution الخاص بـlayer معيّنة بيتغير أثناء الـtraining بسبب الـweight update في الـlayers السابقة، الـshift المستمر ده بيأثر على كفاءة الـtraining لإن الـweight update التالي هيحاول يلافي تأثير التغيير في الـweights في الـlayers الى قبله عشان يقدر يوصل للـminimum cost.
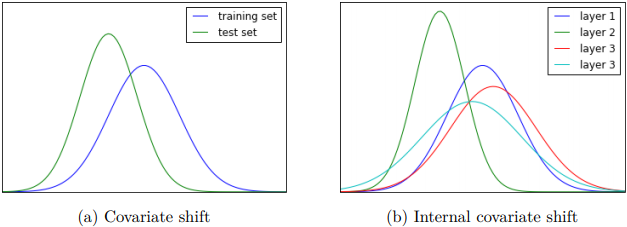
Fig 5: Covariate shift vs. internal covariate shift.
Source: Click here
الحل هنا هو إننا نحاول نثبت الـinput distribution بأكبر شكل ممكن، وده بيتم عن طريق الـBatch normalization: وفيها بنعمل standardization لناتج الـneurons قبل أو بعد الـactivation function بحيث يكون الـdistribution دايماً له نفس الـmean والـvariance بغض النظر عن الـbatch الحالية أو الـweights (لاحظ Figure 6).
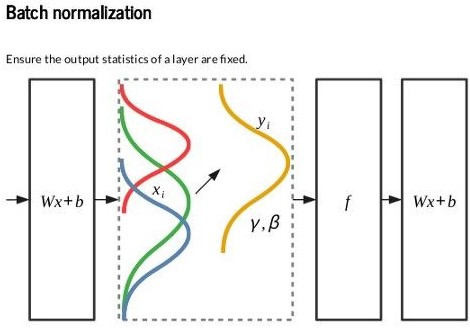
Fig 6: Batch normalization layer. Varying data distributions across batches are normalized.
Source: Click here
وبجانب الـstandardization كمان بنضيف scale & shift parameters بتتعلمهم الـnetwork عشان تقدر تحدد شكل الـdistribution المناسب لها في الـtraining، وبالتالي ممكن تلغي الـbatch norm بنفسها لو مش هتحتاجه.
$\text{Input: Values of } x \text{ over a mini-batch: } B = \{x_{1…m}\}; \text{ Learned parameters: } \gamma,\beta$
$\text{Output: } \{ y_i =BN_{\gamma,\beta}(x_i) \}$
$$ \mu_{B} = \frac{1}{m}\sum_{i=1}^{m} x_i \hspace{17mm} \Rightarrow \text{mini-batch mean} \newline \rule{0mm}{7mm} \sigma_B^2 = \frac{1}{m}\sum_{i=1}^{m} (x_i-\mu_{B})^2 \hspace{1cm} \Rightarrow \text{mini-batch variance} \newline \rule{0mm}{7mm} \hat{x}_i = \frac{x_i-\mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\hspace{16mm} \Rightarrow \text{normalize input} \newline \rule{0mm}{5mm} y_i = \gamma \hat{x}_i + \beta \hspace{17mm} \Rightarrow \text{scale and shift} \newline $$
ورغم إن فيه خلاف حول موضوع الـinternal covariate shift وتأثيره على الـtraining، ده لا ينفي إن الـBatch normalization طريقة فعالة جداً وبتحسن عملية الـtraining بشكل كبير: دلوقتي الـnetwork أصبحت غير معتمدة بشكل كبير على الـweight initialization زى الأول، وكمان الـdistribution أصبح ثابت تقريباً في كل layer وقللت احتمالية وصول الـinput للـsaturation regions، وبالتالي أقدر أستخدم learning rate أكبر وأسرّع الـtraining أكتر، كمان لو استخدمت الـbatch norm قبل الـactivation function فممكن أستغنى عن الـbias، لإن الـshift parameter الموجود في الـbatch norm يؤدي نفس الوظيفة.
وفوق كل ده كمان فالـbatch norm بيضيف نوع من الـregularization على الـnetwork، لإنه بيحسب الـmean والـvariance في كل batch على حدة، وده بيضيف بعض الـnoise على الداتا لإنهم في الغالب مختلفين عن الـmean والـvariance الخاص بتوزيع الداتا بالكامل.
أثناء الـtraining بقدر احسب الـmean والـvariance على كل batch،ايه الى بيحصل في الـtesting؟
أثناء الـtraining ممكن نحسب moving average للـmeans والـvariances الخاصة بكل batch عشان تقرّب من الـmean والـvariance الخاص بالـtraining data، وهم دول الى بستخدمهم في الـbatch norm بعد الـtraining، ومع إن الـbatch norm بيأثر على سرعة الـtesting بسبب الحسابات الإضافية، لكن مزاياه بتعّوض التأثير ده، بالإضافة إلى إننا بعد الـtraining ممكن ندمج الـbatch norm parameters مع الـweights الخاصة بالـlayer الى قبله، وبالتالي نقلل الحسابات ونسرّع زمن الـtesting
If the previos layer computes $XW+b$ then BN layer will compute $\gamma \otimes (XW+b-\mu)/\sigma + \beta$ (ignoring the smoothing term $\epsilon$ in the denominator).
If we define $W'=\gamma \otimes W/\sigma$ and $b'=\gamma \otimes (b-\mu)/\sigma+\beta$, the equation simplifies to $XW'+b'$. So if we replace the previous layer’s weights and biases ($W$ and $b$) with the updated weights and biases ($W'$ and $b'$), we can get rid of the BN layer.
- Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow
- Understanding the difficulty of training deep feedforward neural networks, Xavier Glorot, Yoshua Bengio ; PMLR 9:249–256
- How Does Batch Normalization Help Optimization?
- Batch Normalization: An Incredibly Versatile Deep Learning Tool
- BatchNormalization- a technique that enhances training
- Implementing Batch Normalization in Python
- Understanding Dataset Shift