؟K-meansمشاكل الـ Gaussian Mixture Modelsكيف تحل الـ
؟K-meansوما الذي تضيفه على الـ GMMما هي الـ
الـGaussian Mixture models (GMM) هي عبارة عن probabilistic model بيقدر يعبر عن الـdata distribution وكأنه عبارة عن مجموعة gaussian models متجمعة مع بعض، وممكن نستخدمها كـclustering algorithm مشابه للـk-means . بس إزاي probabilistic model ممكن يعمل clustering للداتا أصلاً؟
الـGMM بيفترض إن الداتا متوزعة في أكتر من gaussian distribution، وهي دى الميزة الى انا بستغلها في الـclustering: انا ممكن اعتبر ان كل Gaussian من دول بيعبر عن cluster واحدة بس من الداتا. لاحظ Fig 1: انا افترضت إن عندي 4 clusters في الداتا ، فاستخدمت GMM فيه 4 Gaussians، فأصبح كل واحد منهم بيعبر عن cluster معينة.
لاحظ Fig 1: انا افترضت إن عندي 4 clusters في الداتا ، فاستخدمت GMM فيه 4 Gaussians، فأصبح كل واحد منهم بيعبر عن cluster معينة.
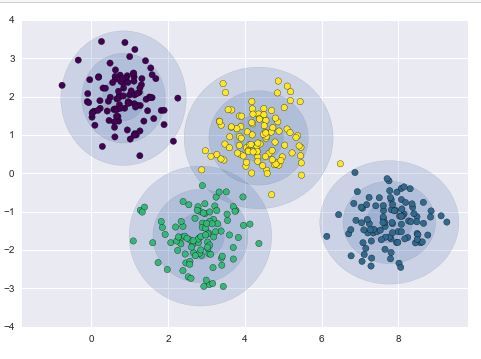
Fig 1: GMM clusters. the data consists of 4 cluster, therefore 4 gaussian components are used.
Source: Click here
طيب ما لو استخدمت الـk-means هلاقي نفس النتيجة، إيه المميز في الـGMM؟
في حالة الصورة الأولى كنت فعلاً هلاقي نتيجة مشابهة، لكن الإضافة الى بتقدمها الـGMM هو إن بقى عندي Probability: الـpoint دلوقتي مش محسوبة على cluster واحد بشكل قاطع، لكن دلوقتي اقدر احسب احتمال وجود نقطة معينة في أي cluster، ده اسمه soft clustering، على عكس الى بتعمله الـk-means وهو الـhard clustering.
الميزة التانية والأكبر هي إن في حالة الـk-means، شكل الcluster بيتحدد بناءً على الـdistance metric الى اختارته في البداية، عكس الـGMM الى بيحدد شكل الـcluster فيه هو الـGaussian parameters الى بيتعلمها في الـtraining، وده بيبعدني عن مشكلة اختيار الـdistance metric المناسب في كل مرة، وكمان بيضيف للـmodel مرونة أكبر لإن ده بيسمحله يغير ابعاد الـcluster في كل dimension على حدة عن طريق الـcovariance matrix الى بيتعلمها، على عكس الـk-means الى هتلاقي ابعاد الـcluster ثابتة على كل الـdimensions.
لاحظ الصورة التانية: في حالة الـk-means الـcluster هتاخد شكل ثابت بغض النظر عن شكل توزيع الـdata، على عكس الـGMM الى قدر يتعلم توزيع الداتا ويتعامل معاها بشكل جيد جداً.
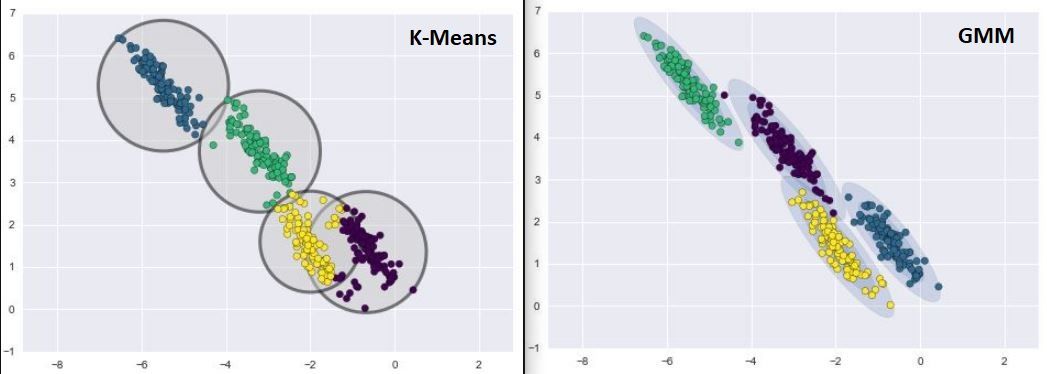
Fig 2: Kmeans clustering vs GMM clustering. Notice how GMM components fit the eliptical shape of the clusters.
Source: Click here
وزى ما قلنا في البداية، في الـGMM النقطة مش بتتحسب على cluster واحدة بس لكن بيكون لها probability لوجودها في كل cluster، أحد الـparameters الى بيتعلمها الـmodel هي في الـmixing coefficients وده بيحدد حجم كل gaussian بناءً على الـpoints density الموجودة فيه وبالتالي بيحدد الـprobability بتاعته.
لاحظ
لو فكرت فيها هتلاقي إنها منطقية: الـgaussian الى فيه نقط اكتر بيكون له وزن أكبر في إجمالي توزيع الداتا ،وخليك فاكر إن الـgaussians دى بتعبر عن توزيع الداتا في الأصل (probability distribution)، وبالتالي لازم يكون مجموع مساحاتهم يساوي 1 عشان يكون الـdistribution صحيح، لذلك بحتاج الـmixing coefficients عشان أحافظ على الخاصية دى.
لو عندي نقطة واقعة بين two clusters هنتعامل معاها ازاي؟
الـMixing coefficient بيمنح الـGaussian الأكبر أفضلية على الـGaussian الصغير، لإن فيه عدد نقط أكتر، لذلك فيه احتمالية أكبر إن النقطة دى تكون تبعه، وده فعلاً الى حصل في النقطة البنفسجية القريبة من الـcluster الاخضر في Fig 2: رغم إنها أقرب للأخضر، بس احتمال وجودها في البنفسجي أكبر، لإن البنفسجي عنده points density أكبر.
الملاحظة الأخيرة هي إن الـGMM مش algorithm مختلف كتير عن الـk-means، لكن ممكن تعتبره الحالة العامة من الـk-means.
لمزيد من المعلومات: